Definición de Espacio muestral: Es el conjunto de los diferentes resultados que pueden darse en un experimento aleatorio, cuando se realiza un experimento, que produce un resultado o una observación, se van a obtener un conjunto de valores. A este conjunto de valores que puede tomar una variable se le denomina espacio muestral.
En otras palabras el espacio muestral es el conjunto de todos los posibles resultados de un experimento aleatorio y se suele representar como E1. A, B, C…= conjuntos.
2. a ,b ,c…= elementos de conjuntos
3. U= unión de conjuntos
4. ∩= intersección de conjuntos
5. A‟= complemento de un conjunto
6. / = dado que
7. \ = diferencia
8. <>= diferente de
9. (Ø )= Conjunto nulo o vacío
10. R= conjunto de los números reales
11. N= conjunto de los números naturales
12. C= conjunto de los números complejos
13. n!= factorial de un numero entero positivo
14. Q= conjunto de los números fraccionarios
15. I= conjunto de los números irracionales
16. c= subconjuntos
17.- { }= llaves.
Unión: La unión de dos sucesos A y B es la probabilidad de que ocurra el suceso A, el suceso B o los dos sucesos a la vez.
El símbolo de la unión de dos sucesos diferentes es una U, por lo que la unión de dos sucesos se expresa con una U en medio de las dos letras que representan los sucesos.
Qué es un diagrama de Venn. (s. f.). Lucidchart. Recuperado 15 de marzo de 2022, de https://www.lucidchart.com/pages/es/que-es-un-diagrama-de-venn#:%7E:text=Estad%C3%ADstica%20y%20probabilidad%3A%20los%20expertos%20en%20estad%C3%ADstica%20usan,distintos%20para%20encontrar%20grados%20de%20similitud%20y%20diferencia.
Estadística, P. Y. (2021, 10 noviembre). ▷ Operaciones con sucesos: unión, intersección y diferencia. Probabilidad y Estadística. Recuperado 15 de marzo de 2022, de https://www.probabilidadyestadistica.net/operaciones-con-sucesos/#:%7E:text=La%20probabilidad%20de%20la%20uni%C3%B3n%20de%20dos%20sucesos,que%204%C2%BB%20en%20el%20lanzamiento%20de%20un%20dado.
Park, M. (2021, 31 mayo). Ejercicios de probabilidad. Espacio muestral y suceso. Smartick. Recuperado 15 de marzo de 2022, de https://www.smartick.es/blog/matematicas/recursos-didacticos/ejercicios-de-probabilidad/#:%7E:text=El%20espacio%20muestral%20es%20el%20conjunto%20de%20todos,E%20%3D%20%7B1%2C%202%2C%203%2C%204%2C%205%2C%206%7D.

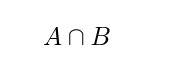






No hay comentarios:
Publicar un comentario