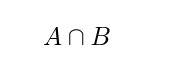2.6 Eventos independientes: Regla de Bayes

Esta regla postulada por Thomas Bayes en 1763 el cual postula la probabilidad condicional de un evento aleatorio A dado B en términos de probabilidad condicional con respecto al evento B que se da por el evento A ósea su probabilidad marginal es solo A.

En una definición más sencilla se puede decir que hay una enorme relevancia entre las probabilidades de A dado en B

Su formula se escribe de la siguiente manera

Ejemplo

1. Tres máquinas denominadas A, B y C, producen un 43%, 26% y 31% de la producción total de una empresa respectivamente, se ha detectado que un 8%, 2% y 1.6% del producto manufacturado por estas máquinas es defectuoso, a. Se selecciona un producto al azar y se encuentra que es defectuoso, ¿Cuál es la probabilidad de que el producto haya sido fabricado en la máquina B?, b. Si el producto seleccionado resulta que no es defectuoso, ¿Cuál es la probabilidad de que haya sido fabricado en la máquina C?


Solución: Para resolver este problema nos ayudaremos con un diagrama de árbol

Ahora se definirán los eventos

D = evento de que el producto seleccionado sea defectuoso (evento que condiciona)
A = evento de que el producto sea fabricado en la máquina A
B = evento de que el producto sea fabricado por la máquina B
C = evento de que el producto sea fabricado por la máquina C

P(B½D) = p(BÇD)/p(D) = p(B)p(D½B)/p(A)p(D½A) + p(B)p(D½B) + p(C)p(D½C)
P(B½D) = (0.26*0.02)/(0.43*0.08 + 0.26*0.02 + 0.31*0.016) = 0.0052/0.04456
=0.116697

ND = evento de que el producto seleccionado no sea defectuoso (evento que condiciona)

A = evento de que el producto sea fabricado en la máquina A
B = evento de que el producto sea fabricado por la máquina B
C = evento de que el producto sea fabricado por la máquina C

P(C½ND)=p(CÇND)/p(ND)=p(C)p(ND½C)/p(A)p(ND½A) + p(B)p(ND½B) + p(C)p(ND½C) = 0.31*0.984/(0.43*0.92 + 0.26*0.98 + 0.31*0.984) = 0.30504/0.95544
=0.31927

REFERENCIAS:

Formula. (s. f.). [Ilustración]. Bayes. https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjZsLgPYouINxt5199wgceTK6N8msPfJNPy7XTHMkZNFwYAeS4QnKzuvzAUmLGu3MI-pthXFwvfD3xfIDcEDAsoJoRWai4aIdPHiLsIF-8Jv_Dx-tH_UoefQ3YixiPfQn2x4FzfUNGE4ig/s275/tba.png

Ramón, I. J. M. (2012c, junio 7). 2.6 Eventos independientes: Regla de Bayes. Blog. Recuperado 15 de marzo de 2022, de https://probabilidadyestadisticaitsav.blogspot.com/2012/06/26-eventos-independientes-regla-de.html

2.5 Probabilidad Condicional

Es decir, la probabilidad condicional es aquella que depende de que se haya cumplido otro hecho relacionado.

Si tenemos un evento, que denominamos A, condicionado a otro evento, al cual denominamos B, la notación sería P(A|B) y la fórmula sería la siguiente:

P(A|B)=P(A ∩ B)/P(B)

Ejemplo

Supongamos que tenemos un aula con 30 alumnos, siendo el 50 % de 14 años y el otro 50% de 15 años. Además, sabemos que 12 integrantes del salón tienen 14 años y usan resaltador en sus libros ¿Cuál es la probabilidad de que un estudiante del salón use resaltador si tiene 14 años?

La probabilidad de que un estudiante use resaltador si tiene 14 años se calcularía de la siguiente forma:

P(A|B)=P(A ∩ B)/P(B)=0,4/0,5=0,8=80%

Las propiedades de la probabilidad condicional son las siguientes:

Esto significa que la probabilidad de A dado B, más la probabilidad del complemento de A (los elementos del universo que no pertenece a A) dado B, es igual a 1.

Esta propiedad implica que si A es un subconjunto de B (o son dos conjuntos iguales), la probabilidad de que ocurra A dado B es 1.

Lo anterior quiere decir que la probabilidad de A es igual a la probabilidad de A dado B por la probabilidad de B más la probabilidad de A, dado el complemento de B por el complemento de B.
REFERENCIAS:

Westreicher, G. (2021, 22 abril). Probabilidad condicional. Economipedia. Recuperado 15 de marzo de 2022, de https://economipedia.com/definiciones/probabilidad-condicional.html

2.4 Probabilidad con técnicas de conteo: Axiomas, Teoremas.

 Axiomas:

Axioma 1:  Si A es un evento  asociado a un espacio muestral S, entonces: 0 <= P(A) <= 1 Esto es, la probabilidad de un evento cualquiera está definida en el intervalo cerrado de 0 a 1.

P(A) --> [ 0 , 1 ]

Axioma 2: La probabilidad del suceso “espacio muestral” es igual a la unidad. Si S es el espacio muestral de un experimento, entonces: 

P(S) = 1

Evento seguro: Es todo suceso donde se tiene la certeza total de que éste ocurre, por lo tanto, su probabilidad es igual a 1. Si el evento “A” es que un ser humano muera su probabilidad será: 

P(A) = 1

Evento Imposible: Es todo evento del cual se tiene la certeza absoluta de que no ocurre, por lo tanto, su probabilidad es cero (nula). Si el evento “A” consiste en obtener un estudiante con una medida de 5 metros de estatura al seleccionarlo de un grupo, su probabilidad será: 

P(A) = 0.

Axioma 3: Si “A” y “B” son dos eventos ajenos, la probabilidad de que ambos ocurran es la suma de sus respectivas probabilidades. 

P(A U B) = P(A) + P (B).

Teoremas:

Teorema 1: Si f es un evento nulo o vacío, entonces la probabilidad de que ocurra f debe ser cero.

p(f)=0

Teorema 2: La probabilidad del complemento de A, Ac debe ser

p(Ac)= 1 – p(A).

Teorema 3: Si un evento A Ì B, entonces la p(A) £ p(B).

Teorema 4: La p( A \ B )= p(A) – p(AÇB)

Teorema 5: Para dos eventos A y B, p(AÈB)=p(A) + p(B) – p(AÇB).

REFERENCIAS:

4 Probabilidad con Técnicas de Conteo. (2017). Blogspot.com. http://probabilidadestadisticaivangamboa.blogspot.com/2017/03/4-probabilidad-con-tecnicas-de-conteo.html

Arias, S., Milvia, L., & Peñaloza De Arias, L. (n.d.). Octubre 2015. http://www.saber.ula.ve/bitstream/handle/123456789/42886/probabilidad_2015.pdf?sequence=2&isAllowed=y

Morales Ramón, J. (2012, June 4). 2.3 Probabilidad con Técnicas de Conteo: Axiomas, Teoremas. Blogspot.com. http://probabilidadyestadisticaitsav.blogspot.com/2012/06/23-probabilidad-con-tecnicas-de-conteo.html

2.3 Probabilidad de Eventos: Definición de espacio muestral, definición de evento, simbología, unión, intersección, diagramas de Venn

Definición de Espacio muestral:     Es el conjunto de los diferentes resultados que pueden darse en un experimento aleatorio, cuando se realiza un experimento, que produce un resultado o una observación, se van a obtener un conjunto de valores. A este conjunto de valores que puede tomar una variable se le denomina espacio muestral.

En otras palabras el espacio muestral es el conjunto de todos los posibles resultados de un experimento aleatorio y se suele representar como E

Por ejemplo, cuando lanzamos una moneda

¿Cuáles son todos los posibles resultados que podemos obtener? Que salga cara o cruz, ¿verdad? En total son dos posibles resultados, por lo que el espacio muestral tiene 2 elementos.

E = {cara, cruz}

Evento:    Un Evento es un resultado particular de un experimento aleatorio. En términos de conjuntos, un evento es un subconjunto del espacio muestral. Por lo general se le representa por las primeras letras del alfabeto. se denota por P(E), se define como el número de eventos elementales que componen al evento E, entre el número de eventos elementales que componen el espacio muestral: 

Cuando se tiene un espacio muestral llamamos, formalmente evento o suceso a cualquier subconjunto del espacio muestral.

Simbología:

1. A, B, C…= conjuntos.
2. a ,b ,c…= elementos de conjuntos
3. U= unión de conjuntos
4. ∩= intersección de conjuntos
5. A‟= complemento de un conjunto
6. / = dado que
7. \ = diferencia
8. <>= diferente de
9. (Ø )= Conjunto nulo o vacío
10. R= conjunto de los números reales
11. N= conjunto de los números naturales
12. C= conjunto de los números complejos
13. n!= factorial de un numero entero positivo
14. Q= conjunto de los números fraccionarios
15. I= conjunto de los números irracionales
16. c= subconjuntos
17.- { }= llaves.


Unión:    La unión de dos sucesos A y B es la probabilidad de que ocurra el suceso A, el suceso B o los dos sucesos a la vez.

El símbolo de la unión de dos sucesos diferentes es una U, por lo que la unión de dos sucesos se expresa con una U en medio de las dos letras que representan los sucesos.

A u B

La probabilidad de la unión de dos sucesos es igual a la suma de la probabilidad de ocurrencia de cada suceso menos la probabilidad de la intersección de ambos sucesos.

Intersección:     La intersección de dos eventos A y B, denotada por A B y leída “A y B”, es el evento que consiste en todos los resultados que están tanto en A como en B

Diagramas de Venn:    Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. Este se basa en la teoría de conjuntos y es muy habitual en matemáticas. Además, también ha demostrado ser útil en el llamado razonamiento diagramático que representa los diferentes conceptos a través de figuras

REFERENCIAS:

Qué es un diagrama de Venn. (s. f.). Lucidchart. Recuperado 15 de marzo de 2022, de https://www.lucidchart.com/pages/es/que-es-un-diagrama-de-venn#:%7E:text=Estad%C3%ADstica%20y%20probabilidad%3A%20los%20expertos%20en%20estad%C3%ADstica%20usan,distintos%20para%20encontrar%20grados%20de%20similitud%20y%20diferencia.

Estadística, P. Y. (2021, 10 noviembre). ▷ Operaciones con sucesos: unión, intersección y diferencia. Probabilidad y Estadística. Recuperado 15 de marzo de 2022, de https://www.probabilidadyestadistica.net/operaciones-con-sucesos/#:%7E:text=La%20probabilidad%20de%20la%20uni%C3%B3n%20de%20dos%20sucesos,que%204%C2%BB%20en%20el%20lanzamiento%20de%20un%20dado.

Park, M. (2021, 31 mayo). Ejercicios de probabilidad. Espacio muestral y suceso. Smartick. Recuperado 15 de marzo de 2022, de https://www.smartick.es/blog/matematicas/recursos-didacticos/ejercicios-de-probabilidad/#:%7E:text=El%20espacio%20muestral%20es%20el%20conjunto%20de%20todos,E%20%3D%20%7B1%2C%202%2C%203%2C%204%2C%205%2C%206%7D.

2.2 Teoría elemental de probabilidad

El Cálculo de Probabilidades se ocupa de estudiar ciertos experimentos que se denominan aleatorios, cuya característica fundamental es la incertidumbre del resultado

La manera mas antigua de medir la incertidumbre es con el concepto clásico de probabilidad, ya que este se desarrollo originalmente en relación con los juegos de azar y por si mismo lleva una relación más viable entre posibilidades y probabilidades.

Este tipo de información es insuficiente cuando se necesita un conocimiento más profundo de un fenómeno aleatorio

El concepto clásico de probabilidad se aplica solo cuando todos los resultados posibles son igualmente probables

“Si para un evento A hay n resultados igualmente probables, de las cuales f son del tipo que nos interesa, la probabilidad de que ocurra un resultado de este tipo es:

                                                                        P(a)=f / n

Ejemplo

Supongamos que un suceso E tiene h posibilidades de ocurrir entre un total de n posibilidades, cada una de las cuales tiene la misma oportunidad de ocurrir que las demás.


Entonces, la probabilidad de que ocurra E (0 sea un éxito) se denota por

p = Pr{E}=h/n

La probabilidad de que no ocurra E (0 sea, un fracaso) se denota por

REFERENCIAS:

Hernandez, R. (s. f.). Teoría elemental de la Probabilidad. Prezi.Com. Recuperado 15 de marzo de 2022, de https://prezi.com/vay2j2mznroq/teoria-elemental-de-la-probabilidad/

Ramón, I. J. M. (2012a, mayo 27). 2.1 Teoría elemental de probabilidad. Blog. Recuperado 15 de marzo de 2022, de https://probabilidadyestadisticaitsav.blogspot.com/2012/05/21-teoria-elemental-de-probabilidad.html

 

2.1.7 Teorema del Binomio

También llamado binomio de Newton, este expresa la enésima potencia de un binomio como un polinomio. El desarrollo del binomio ( a + b)^n posee singular importancia ya que aparece con mucha frecuencia en Matemáticas.

Formula general

Sea un binomio de la forma (a +b)^n.

Entendiendo esto tenemos los siguientes casos:

De lo anterior, se aprecia que:


a) El desarrollo de (a + b)^n tiene n +1 términos.
b) Las potencias de a empiezan con n en el primer término y van disminuyendo en cada término, hasta cero en el último.
c) Las potencias de b empiezan con exponente cero en el primer término y van aumentando en uno con cada término, hasta n en el último.
d) Para cada término la suma de los exponentes de a y b es n .
e) El coeficiente del primer término es uno y el del segundo es n .
f) El coeficiente de un término cualquiera es igual al producto del coeficiente del término anterior por el exponente de a dividido entre el número que indica el orden de ese término.
g) Los términos que equidistan de los extremos tienen coeficientes iguales.

REFERENCIAS:

Ramón, I. J. M. (2012, 27 mayo). Teorema del Binomio. Blog. https://probabilidadyestadisticaitsav.blogspot.com/2012/05/17-teorema-del-binomio.html

P. (2022, 9 enero). ▷ Binomio de Newton (o teorema del binomio). Polinomios. Recuperado 15 de marzo de 2022, de https://www.polinomios.org/binomio-de-newton-o-teorema-del-binomio-formula-y-ejercicios-resueltos/

2.1.6 Diagramas de Árbol

Un diagrama de árbol es una representación gráfica de los posibles resultados de un experimento que tiene varios pasos. Nos permite calcular la probabilidad de que ocurra un evento de una manera muy sencilla. Se utiliza tanto cuando los sucesos son independientes como dependientes.

En términos generales, el diagrama de árbol sirve como una herramienta para planificar varias estrategias e identificar la mejor, a fin de alcanzar un determinado objetivo ya que nos ayuda a cuantificar todas las opciones para elegir las más efectivas, e ir descartando las que no son tan efectivas o deseadas

Ejemplo

Una moneda tiene en sus caras un gato y un perro. Se se lanza 2 veces la moneda, calcular:

a) la probabilidad de obtener 2 gatos.

REFERENCIAS:

Probabilidad. (s. f.). [Ilustración]. probabilidad de moneda. https://matemovil.com/wp-content/uploads/2019/07/probabilidad-diagrama-de-%C3%A1rbol-1.jpg

J. (2021, 1 enero). Diagrama de árbol (probabilidades) | Matemóvil. MateMovil. Recuperado 15 de marzo de 2022, de https://matemovil.com/diagrama-de-arbol-probabilidades/

2.1.5 Combinaciones

Es todo arreglo de elementos en donde no nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.

A diferencia de las permutaciones, las combinaciones solo nos interesa formar grupos y el contenido de los mismos.

La fórmula para contar el número de r combinaciones de objetos de un conjunto de n objetos es:

Ejemplo 1: ¿Cuántos pasteles se pueden formar a partir de 9 ingredientes disponibles?


Solución: Se requieren 6 ingredientes para formar un pastel, por lo que, en este caso se tiene que.


                                                                    n = 9

                                                                    r = 6

de manera que 

REFERENCIAS: 

Ramón, I. J. M. (2019, 16 marzo). 1.5 Combinaciones. Blog. Recuperado 15 de marzo de 2022, de https://probabilidadyestadisticaitsav.blogspot.com/2012/05/15-combinaciones.html

Técnicas de conteo: tipos, cómo utilizarlas y ejemplos. (s. f.). Combinaciones. Recuperado 15 de marzo de 2022, de https://psicologiaymente.com/miscelanea/tecnicas-de-conteo

2.1.4 Permutaciones

 Antes de empezar, tenemos que tener en cuenta de manera muy clara la diferencia entre las permutaciones y las combinaciones 

Las combinaciones son arreglos de elementos cuyo orden no es importante o no cambia el resultado final

Mientras que las permutaciones el orden si es de suma importancia, además hay n cantidad de elementos distintos y se selecciona una cantidad de ellos, que sería r.

La fórmula que se utilizaría sería la siguiente:

nPr = n!/(n-r)! 

Ejemplo:

Hay un grupo de 10 personas y hay un asiento en el que solo pueden caber cinco, ¿de cuántas formas se pueden sentar?

Se haría lo siguiente:

10P5=10!/(10-5)!=10 x 9 x 8 x 7 x 6 = 30.240 formas diferentes de ocupar el banco.

REFERENCIAS:

Técnicas de conteo: tipos, cómo utilizarlas y ejemplos. (s. f.). Permutaciones. Recuperado 15 de marzo de 2022, de https://psicologiaymente.com/miscelanea/tecnicas-de-conteo

Combinaciones. (s. f.). [Ilustración]. Combinación de figuras. https://es-static.z-dn.net/files/dd9/6fcd2a7ad7d5998c6b019099c81146ac.png

2.1.3 Notación Factorial

La notación factorial se usa para calcular el producto de los primeros n números naturales, es decir, los enteros positivos, comenzando desde el 1 hasta el valor de n

Se denota mediante un signo de admiración y se llama n factorial



                                                    "n! = 1⋅2⋅3…. (n-1)⋅n"




Ejemplo

Obtener el factorial de 5!

                                                5!= (1)(2)(3)(4)(5) = 120

Al realizar dichas multiplicaciones tenemos que el factorial de 5 es 120

En un caso practico esto seria útil para saber que tantas combinaciones posibles tenemos para acomodar o hacer algo

REFERENCIAS:

Notación Factorial. (s. f.). [Ilustración]. Factorial 6. https://th.bing.com/th/id/R.82ed953840b404eb601a0f0eff73bf3d?rik=OCoEqHpkKYAtdQ&riu=http%3a%2f%2f1.bp.blogspot.com%2f-zZrmNqjd48s%2fTwRI170OvDI%2fAAAAAAAAAUU%2fQbOz0jkHn-s%2fw1200-h630-p-k-no-nu%2ffactorial%2bde%2bun%2bnumero%2bnatural.PNG&ehk=2s0iRXOLII8J1JTDEfDSvVLN%2bR4DLV3mNiZXLSIoIEQ%3d&risl=&pid=ImgRaw&r=0

Zapata, F. (2020, 12 octubre). Notación factorial: concepto, ejemplos y ejercicios. Lifeder. Recuperado 15 de marzo de 2022, de https://www.lifeder.com/notacion-factorial/#:%7E:text=La%20notaci%C3%B3n%20factorial%20se%20usa%20para%20calcular%20el,signo%20de%20admiraci%C3%B3n%20y%20se%20llama%20n%20factorial%3A

2.1.2 Principio Multiplicativo

Regla especial de la multiplicación La regla especial de la multiplicación requiere que dos eventos, A y B, sean independientes, y lo son si el hecho de que uno ocurra no altera la probabilidad de que el otro suceda


                                                                    P(A y B) P(A)P(B)

Este tipo de técnica de conteo, junto con el principio aditivo, permiten comprender fácilmente y de forma práctica cómo funcionan estos métodos matemáticos.

Si un evento, llamémoslo N1, puede ocurrir de varias formas, y otro evento, N2, puede ocurrir de otras tantas, entonces, los eventos conjuntamente pueden ocurrir de N1 x N2 formas.

Este principio se utiliza cuando la acción es secuencial, es decir, está conformada por eventos que ocurren de forma ordenada, como son la construcción de una casa, el elegir los pasos de baile en una discoteca o el orden que se seguirá para preparar un pastel.

Ejemplo:

En un restaurante, el menú consiste en un plato principal , un segundo y postre. De platos principales tenemos 4, de segundos hay 5 y de postres hay 3.

Entonces, N1 = 4; N2 = 5 y N3 = 3.

Así pues, las combinaciones que ofrece este menú serían 4 x 5 x 3 = 60

REFERENCIAS:

Rubio, N. (2022, 30 enero). Técnicas de conteo: tipos, cómo utilizarlas y ejemplos. Probabilidad y mente. Recuperado 14 de marzo de 2022, de https://psicologiaymente.com/miscelanea/tecnicas-de-conteo

Comida china. (s. f.). [Ilustración]. representacion. https://www.bing.com/images/search?view=detailV2&ccid=qSGlkxfQ&id=B190864BCB35D6F5E363CA17BC00300823AC72E2&thid=OIP.qSGlkxfQIdLY8ujVRFHWbwHaKd&mediaurl=https%3A%2F%2Fwww.kuwaitup2date.com%2Fwp-content%2Fuploads%2F2015%2F06%2FWokhay-Ramadan-725x1024.jpg&exph=1024&expw=725&q=menus+de+comida&simid=608007824225169466&form=IRPRST&ck=5E3E05CE5D8D561A5D241B8165A55724&selectedindex=4&ajaxhist=0&ajaxserp=0&cdnurl=https%3A%2F%2Fth.bing.com%2Fth%2Fid%2FR.a921a59317d021d2d8f2e8d54451d66f%3Frik%3D4nKsIwgwALwXyg%26pid%3DImgRaw%26r%3D0&pivotparams=insightsToken%3Dccid_YjOn5Cfp*cp_9982C87BCEE0EE9B2965458B5BC922EE*mid_22FA9D2ACF84C882A985EBBEE543D4F0652B501D*simid_607994922137225390*thid_OIP.YjOn5Cfp6A8qz7NoB5d0iwHaHa&vt=0&sim=11&iss=VSI&ajaxhist=0&ajaxserp=0

2.1.1 Principio Aditivo

En este tipo de conteo se caracteriza por que se suman las distintas formas en las que pueden ocurrir cada evento.

Esto quiere decir que si la primera actividad puede ocurrir de M formas, la segunda de N y la tercera L, entonces, de acuerdo a este principio, sería M + N + L.

Ejemplo:

Queremos comprar chocolate, habiendo tres marcas en el supermercado: A, B y C.

El chocolate A se vende de tres sabores: negro, con leche y blanco, además de haber la opción sin o con azúcar para cada uno de ellos.

El chocolate B se vende de tres sabores, negro, con leche o blanco, con la opción de tener o no avellanas y con o sin azúcar.

El chocolate C se vende de tres sabores, negro, con leche y blanco, con opción de tener o no avellanas, cacahuete, caramelo o almendras, pero todos con azúcar.

En base a esto, la pregunta que se pretende responder es: ¿Cuántas variedades distintas de chocolate se pueden comprar?

W = número de formas de seleccionar el chocolate A.

Y = número de formas de seleccionar el chocolate B.

Z = número de formas de seleccionar el chocolate C.

El siguiente paso consiste en una simple multiplicación.

W = 3 x 2 = 6.

Y = 3 x 2 x 2 = 12.

Z = 3 x 5 = 15.

W + Y + Z = 6 + 12 + 15 = 33 variedades de chocolate diferentes

REFERENCIAS:

Rubio, N. (2022, 30 enero). Técnicas de conteo: tipos, cómo utilizarlas y ejemplos. Probabilidad y mente. Recuperado 14 de marzo de 2022, de https://psicologiaymente.com/miscelanea/tecnicas-de-conteo

Chocolate. (s. f.). [Fotografía]. Imagen de prueba. https://th.bing.com/th/id/R.ff64ee215e3145ddba96034ee0fd19e1?rik=yAFSm53jz4iWZQ&pid=ImgRaw&r=0

2. Fundamentos de la Teoría de Probabilidad

 2.1 TÉCNICAS DE CONTEO

Son estrategias matemáticas usadas en probabilidad y estadística que permiten determinar el número total de resultados a partir de combinaciones.

Este tipo de técnicas se utilizan cuando es prácticamente imposible o demasiado pesado hacer de forma manual combinaciones de diferentes elementos y saber cuántas de ellas son posibles

Ejemplo:

Si se tienen cuatro sillas, una amarilla, una roja, una azul y una verde, ¿Cuántas combinaciones de tres de ellas se pueden hacer ordenadas una al lado de la otra?

Se podría resolver este problema haciéndolo manualmente, pensando en combinaciones como azul, rojo y amarillo; azul, amarillo y rojo; rojo, azul y amarillo, rojo, amarillo y azul… Pero esto puede requerir mucha paciencia y tiempo,  para eso haríamos uso de las técnicas de conteo, siendo para este caso necesaria una permutación.

Referencia:

Rubio, N. (2022, 30 enero). Técnicas de conteo: tipos, cómo utilizarlas y ejemplos. Probabilidad y mente. Recuperado 14 de marzo de 2022, de https://psicologiaymente.com/miscelanea/tecnicas-de-conteo

Conteo. (s. f.). [Ilustración]. Imagen. https://th.bing.com/th/id/OIP.K2g5NI21rVW2eN8Wca16nwHaEw?pid=ImgDet&rs=1